DEFINITION OF WHOLE NUMBERS WITH EXAMPLES | VIDEO | TYPES IN 2024

DEFINITION OF WHOLE NUMBERS WITH EXAMPLES | VIDEO | TYPES IN 2024

DEFINITION OF WHOLE NUMBERS WITH EXAMPLES | Let's learn what is the definition of whole numbers in math & what are real whole numbers in Hindi.

 

Definition of whole numbers with examples

WHAT IS THE DEFINITION OF WHOLE NUMBERS IN MATH WITH TYPES/PROPERTIES/SYMBOL/DEMO?

 

Whole numbers are numbers that don’t have fractions or decimals. They’re just whole numbers. The number 1 is a whole number, as is 2, 3, 4, and so on.

 

When you’re working with whole numbers, there are a few things you need to remember. First, always add the numbers together in order to get the total.

 

For example, if you have 1 + 2 + 3 = 6. Second, to subtract one whole number from another, you need to start with the largest number and count down.

 

So, if you’re subtracting 5 – 3, you would start with 5 and count down to 3, which would give you 2. Lastly, when you’re multiplying or dividing whole numbers, the order of the numbers doesn’t matter. For example, 3 X 4 is the same as 4 X 3.

 

WHAT ARE WHOLE NUMBERS?

 

Whole numbers are positive integers that start at 1 and go up to infinity.

The set of whole numbers is {1, 2, 3, 4, 5, ...}.

 

WHOLE NUMBERS EXAMPLES

Hold numbers in our day to day life. To count things we use numbers like 1,2,3,4… The collection of these kinds of numbers like 1234, and so on. We call this collection of numbers as natural numbers.

 

We represent the set of natural numbers with the letter N.

 

N= {1, 2, 3, 4..}

 

So N is the natural numbers 1,2,3,4…. So every natural number has a successor see, for example, 3 has got a successor 4.

 

If you see two it has got a successor 3. And in the same way, the natural numbers that except one are the natural numbers they have a predecessor three is having two as a predecessor & 4 is having 3.

 

But whereas 1 is having a successor, but it is not having a predecessor number. Now, if we add zero, the collection of natural numbers, this is a collection of natural numbers.

 

N= {1, 2, 3, 4..}

 

 

If we add 0 to the collection, we call this set the natural numbers, add zero with zero we call it as whole numbers and we denote it with the letter W.

 

W= {0, 1,2,3,4..}

 

So this is so on. So whole numbers are the set of natural numbers, zero including zero, we call it as whole numbers. So in this chapter, we're going to learn about this whole numbers.

 

Representation of whole numbers on the number line –

 

So first, let us see a number line. Now first, draw a line and mark a point as zero on the line now with equal distances onto the right side of the line, keep on marking till the end of the line.

So we mark 12345678910 and so on as given below image till N.

Definition of whole numbers with examples

So this is the number line we have made. So now we adsorbed the number line here, every number on this number line has got a successor towards its right side.

 

So six is having its successor on the right side 7. So this is a number line drawn with whole numbers. Now we'll see that addition of numbers on the number line.

 

Whole number by the addition of numbers on the number line-

 

So here we are going to support numbers using a number line here the initial union is two plus three.

 

2+3

 

So how to do this using a number line the first digit is 2. So let us start at to go to the number line and begin from 2 +3.

 

So that is we have to move. Now in which direction do we have to move either to the right or left. Here we have to move towards the right.

 

Doing addition, two plus three. So we have to move to the right side from two how many positions we have to move 2+3. So we have to move 3 positions towards the right side from 2 starting at two.

 

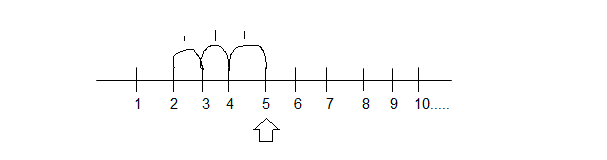Definition of whole numbers with examples

So now we reached 5. That means 2 plus 3 equal to 5.

 

2+3=5

 

So this way use the number line to do additions. Let us see the subtraction on a number line.

 

Let us subtract some whole numbers using a number line. Subtraction of whole numbers on a number line.

 

So six minus two 6-2 the first digit is six now go to six on the number line two, minus 2 we have to move two positions on which direction to write or left.

 

This is a subtraction we have to move to the left side if it is addition, right side subtraction left, how many positions two because it is six minus two from six towards left two positions.

 

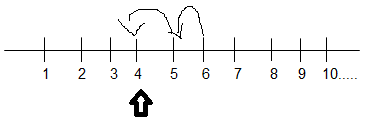Definition of whole numbers with examples

So we reach 6-2= 4 is a win subtract whole numbers on a number line.

 

Multiplication of the whole number with example

 

multiplication on numbers like say, for example, 2x4 how to do this multiplication of whole numbers on number line two into four 2x4.

 

That means 2 positions four times 2positions to the right side. How many times 4 times. So we reached 8.

 

Definition of whole numbers with examples

So we are moving the right side every time to two positions. How many times because it is 2x4. So we got 8. This is a multiplication of the whole number with an example.

Properties of whole numbers

 

Let us see 5+7=12.

 

So here 5 is a whole number. 7 is also a whole Number. 3+4=7, plus four equal to seven. 3 is a whole number and 4 is the upper so 7 number is that whole number.

 

So, Here is what do we understand? From these examples? The sum of two whole numbers gives you so here the sum of any two whole numbers will be a whole number.

 

So this is one of the properties. Now let me see out of the number 2x3=6, 2 is a whole number 3 is also a whole number 6 is a whole number.

 

4X5=20

 

 So here also all the three whole numbers are so here the product or the multiplication of any two whole numbers multination of the whole number.

 

So here in the previous one, we have seen that the sum of any two whole numbers gives rise to a whole number.

Here the multiplication of any two whole numbers gives rise to a whole number. We can get from these two examples we can say that the collection of whole numbers is put under addition and multiplication, but this is not possible in subtraction and division.

 

Subtraction of whole numbers with an example

 

Let us see let it let us see here a subtraction 5-7 five minus seven. If you remove 5-7. So from five if you remove seven you will get -2.

 

So these minus numbers are not the whole numbers collection of natural numbers and zero.

 

So this is not a whole number. So a whole number minus a whole number does not become a whole number.

 

Division of whole numbers with an example

 

Look at Division five divided by two 5÷2. So this is a 5/2 by two, it is not a whole number.

 

Whereas in addition, and in multiplication, we find that the sum of two whole numbers becomes a whole number addition, the product of two whole numbers always becomes a whole number.

 

3+5=8

5+3=8

 

Now let us look at your numbers. Say, for example, three plus five equal to five is equal to eight. So here we have two examples three plus five equal to eight and five plus three.

 

So what is here the order of this whole number pay is changed. The rest is the same, the same, but the order is changed here three plus five here five plus three, but the result is the same.

 

So the sum of the whole numbers the ordering paid is changed the sum the value will be the same. This property is known as commutative property. So the whole numbers are committed to in addition.

 

Now let us see multiplication. Two into three equal to six, three into two equal to six.

 

2x3=6

3x2=6

 

Here, we have two whole numbers multiply your product and hear the same numbers but the order of the payer even though the order of the pay is changing, the result is the same.

 

So the whole numbers are commutative in the case of multiplication.

 

Commutative property of whole numbers

 

Let us see the addition of two whole numbers three plus five equal to eight, five plus three equal to eight.

 

3+5=8

5+3=8

 

We have an addition of two whole numbers t plus five. In both the cases the whole thing, but the pay that is changed here is the same pay three, five, even five, three, the order is changed.

 

The order is changed in the addition of whole numbers, the result will be the same. So we say that this property is commutative property.

 

Here we say that the addition is commutative in whole numbers. So in whole numbers, the addition is commutative.

 

Now let us look at the multiply 2x3=6, 3x2=6. So here same value of the product. But here the numbers are changed.

 

So the pay order is changing. In the case of multiplication even though the order of the paid the result is the same it is equally so multiplication is also commutative. Multiplication of whole numbers is commutative.

 

So we can say that addition and multiplication are commutative.

Associativity of whole numbers

 

 Now let us see three plus four plus 523 plus four seven plus five is equal to 12.

 

Now the same arrangement, three plus four plus five.

 

(3+4)+5=7+5=12

 

So, the same things can be arranged like –

 

3+ (4+5) =3+9=12

 

In the second case, first four and five we add two three. So we got 12. Both cases are the same even though here the arrangement and addition is different.

 

So here we call this property as associative property. So in the addition of whole numbers are associative.

 

Associatively in multiplication

Now let us see the associativity in multiplication. Let us see the associativity of multiplication in whole numbers.

 

So here we have three dots in six cells. So three into two columns. The pattern looks like in below image.

So we have in every box we have six coins, three coins. So two columns, three coins into two columns, three coins into two-three into two.

 

 

Definition of whole numbers with examples

6+6+6=18

 

So this is the pattern. Here if you look in a different rendering pattern, three columns, each four, so we write 4x3, sequentially.

 

Associativity of multiplication for whole numbers

Let us see the associativity of multiplication for whole numbers.

Some dots are arranged in a box as shown in the below image. so this box is having two columns and three dots has each column into two.

 

(3x2) x 4

6x4=24

 

Kind of the same here is a different arrangement of four dots in each column as shown below figure with example.

(4x3) x 2

12x2=24

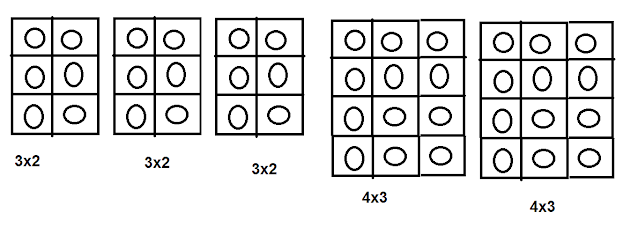Definition of whole numbers with examples

Four into three or four boxes are there. Three into two into four. In the same way here two boxes, four into two, three to two total result is 18. So here in both cases, the answer is the same the value is the same, but the numbers that we are multiplying at the beginning are different.

 

Associative property of multiplication for whole numbers

So what is the associative property of multiplication for whole numbers? So we find that addition and multiplication are associative over whole numbers.

Now let us find this example.

 

5x9x2x2x3x5

 

Find the product of five into nine into two into two into my applying commutative property we change the order of these numbers

 

5x2x92x5x3

(5x2) x 9 x (2x5) x 3

10x9x10x3

=90x30

=2700

 

So now this is commutative property. We are committed to the property. So now we use the associative property five into two into nine into two into five into three as an associative property.

 

So, this is the associative property five into nine and three second nines 90x30. so the answer is 2700.

So, in this way by applying this committee to property and associative property we could do this multiplication as even a simple and easy way to directly find out the answer.

 FAQs

HOW MANY WHOLE NUMBERS ARE THERE UP TO 100?

If you are searching what are the whole numbers are till 100? So, here I have shared a complete list of the whole number which starts from 0 to 100. Actually, there are 101 whole numbers that are there from 0 to 100.

NOTE- As whole numbers are all counting numbers including zero.

LIST OF WHOLE NUMBERS UP TO 100

0	51
1	52
2	53
3	54
4	55
5	56
6	57
7	58
8	59
9	60
10	61
11	62
12	63
13	64
14	65
15	66
16	67
17	68
18	69
19	70
20	71
21	72
22	73
23	74
24	75
25	76
26	77
27	78
28	79
29	80
30	81
31	82
32	83
33	84
34	85
35	86
36	87
37	88
38	89
39	90
40	91
41	92
42	93
43	94
44	95
45	96
46	97
47	98
48	99
49	100
50

HOW CAN YOU USE WHOLE NUMBERS IN YOUR EVERYDAY LIFE?

 

You can use whole numbers to measure things, count things, and add or subtract things.

 

WHAT IS THE IMPORTANCE OF WHOLE NUMBERS?

 

Whole numbers are important because they are the foundation for all other types of numbers. They are the building blocks for all mathematical operations and concepts.

 

WHAT HAPPENS WHEN YOU DIVIDE A WHOLE NUMBER BY ANOTHER WHOLE NUMBER?

 

An answer is a whole number.

 

 

HOW CAN YOU FIND THE SQUARE ROOT OF A WHOLE NUMBER?

 

There is no easy way to find the square root of a whole number. However, you can use a calculator to approximate the square root of a whole number.

 

WHOLE NUMBERS FROM 0?

 

Whole numbers are numbers that have no decimal places. They are the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

 

WHY IS ZERO A WHOLE NUMBER?

 

Zero is a whole number because it can stand alone as a number. It is not a fraction or a decimal, so it is considered a whole number.

 

WHAT ARE THE WHOLE NUMBERS FROM 1 TO 100?

 

The whole numbers 1 to 100 are:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 18 , 19 20 , 21 22 , 23 24 , 25 26 , 27 28 , 29 30 , 31 32 , 33 34 , 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 }

 

HOW DO I FIND A WHOLE NUMBER?

 

To find a whole number, you can use a variety of methods, depending on the type of number you are looking for.

 

For example, if you are looking for a specific number like 42, you could use a search engine to find it. However, if you are looking for a random whole number, you could use a random number generator.

 

WHAT IS NOT A WHOLE NUMBER?

A whole number is an integer that is greater than or equal to zero. A number that is not a whole number is a fraction.

 

WHAT IS THE PROPERTY OF WHOLE NUMBERS?

 

The properties of whole numbers are that they are integers greater than or equal to zero.

 

They have no fractional parts or decimal points, and they cannot be negative.

 

Some of the properties of whole numbers include commutativity, associativity, identity, closure, and distributivity.

 

WHAT IS 2/3 AS A WHOLE NUMBER?

2/3 is not a whole number.

 

WHAT IS THE SMALLEST WHOLE NUMBER?

The smallest whole number is 0.

 

IS 13 A WHOLE NUMBER?

Yes, 13 is a whole number.

 

WHICH IS THE LARGEST WHOLE NUMBER?

There is no largest whole number.

 

IS NEGATIVE 1 A WHOLE NUMBER?

No, negative 1 is not a whole number.

 

HOW MANY TYPES OF PROPERTIES ARE THERE IN THE WHOLE NUMBER?

 

There are 6 types of properties in whole numbers they are –

1. Even numbers,

2. Odd numbers,

3. Prime numbers,

4. Composite Numbers,

5. Positive integers

6. Negative integers.

 

Even numbers are those which are divisible by 2. odd numbers are those which are not divisible by 2. Prime numbers are those which have only two factors, 1 and the number itself while composite numbers have more than two factors. Positive integers are greater than zero while negative integers are less than zero.

 

WHAT IS THE SYMBOL FOR WHOLE NUMBERS?

The symbol for whole numbers is the English letter W.

 

WHAT IS THE DIFFERENCE BETWEEN WHOLE NUMBERS AND COUNTING NUMBERS?

The difference between whole numbers and counting numbers is that whole numbers start at zero, while counting numbers start at one.

This means that if you're counting objects, you would start at one rather than zero.

 

WHAT IS THE DIFFERENCE BETWEEN A WHOLE NUMBER AND A FRACTION?

A whole number is an integer, meaning it has no fractional component. A fraction is a rational number, meaning it has both an integer component and a fractional component.

 

An integer is a rational number with no fractional component, in other words, a number that can be represented as an integer time some power of 10.

 

One way to think about it is that a whole number is a number that can be represented by an infinite decimal expansion with no fractional component, while a fraction is a number that can be represented by an infinite decimal expansion with both an integer and fractional component.

 

WHAT IS THE DIFFERENCE BETWEEN DECIMAL AND WHOLE NUMBERS?

Decimal numbers are numbers that have a fractional component, while whole numbers are numbers that do not have a fractional component.

 

DIFFERENCE BETWEEN NATURAL NUMBERS AND WHOLE NUMBERS

 

Whole numbers are all natural numbers including 0/ZERO.

 

 

ADDITION OF WHOLE NUMBERS

 

We can add whole numbers by aligning them according to place value and then summing up the digits in each place.

 

To add two whole numbers with different place values, we need to line them up on a number line so that the one's digits are lined up, the tens digits are lined up, and so forth. This will ensure that the digits are in their correct places before we start adding.

 

Adding two whole numbers is straightforward. If the numbers being added have the same place value, then we simply need to sum those digits and carry them over to the next column if necessary.

 

If one of the numbers has a larger place value than the other, we can align them such that only their least significant digits (one's digit) are lined up. The rest of that number is shifted by the appropriate amount so that it is correctly aligned with its counterpart from the other number. Once again, we add only those digits in each column and carry over where needed:

 

SUBTRACTION OF WHOLE NUMBERS

 

The algorithm for subtracting whole numbers from one another is instead based on addition. We subtract by first reversing subtraction into addition, then adding, and finally reversing back into subtraction once more. 

This assumes you already know how to subtract two whole numbers without utilizing a number line (borrowing or regrouping). Subtracting using a number line can be done, but this doesn’t lend itself well to longer equations so hope you've practiced your subtraction without a number line! Read the rest of the lessons below to see just how this is done!

 

In the algorithm to subtract one whole number from another, you first find their difference by adding them and reversing the sign. Once you have this difference, you can follow the algorithm for subtraction given in the additive functions sub-lesson. For example: 4 - 8 = 9 - 8; 8 + (-4) = 4 - 8 = 11 - 4 = 16 - 11. Here’s a sample algorithm (using list form).

 

Conclude- Here I have explained in full detail about what is the definition of whole numbers with examples, how many whole numbers are there what are the properties of whole numbers in English with a Hindi live video for beginners who are in any class in 2023.